What Are The Coefficients A B And C Of The Parabola Y Ax 2 Bx C That Passes Through The Point 3 13 And Tangent To The Line 8x Y 15 At 2 1 Quora
In termini più generali una parabola è una conica non degenere In questo formulario presentiamo la definizione e tutte le principali formule della parabola nel piano cartesiano, distinguendo tra parabole ad asse di simmetria verticale e ad asse di simmetriaSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more
Parabola y=x^2 1 y=19-(x)^2
Parabola y=x^2 1 y=19-(x)^2-Free Parabola calculator Calculate parabola foci, vertices, axis and directrix stepbystep This website uses cookies to ensure you get the best experienceUse la forma de vértice, y = a ( x − h) 2 k y = a ( x h) 2 k para determinar los valores de a a, h h, y k k a = 1 a = 1 h = 0 h = 0 k = − 1 k = 1 Dado que el valor de a a es positivo, la parábola se abre hacia arriba Se abre hacia arriba Encuentra el vértice ( h, k) ( h, k)
Solved Find The Equation Of The Parabola With Its Focus At 7 6 And Its Directrix At Y 4 Question 17 Options A Y 4 X 5 7 B Y 4 X 7 Course Hero
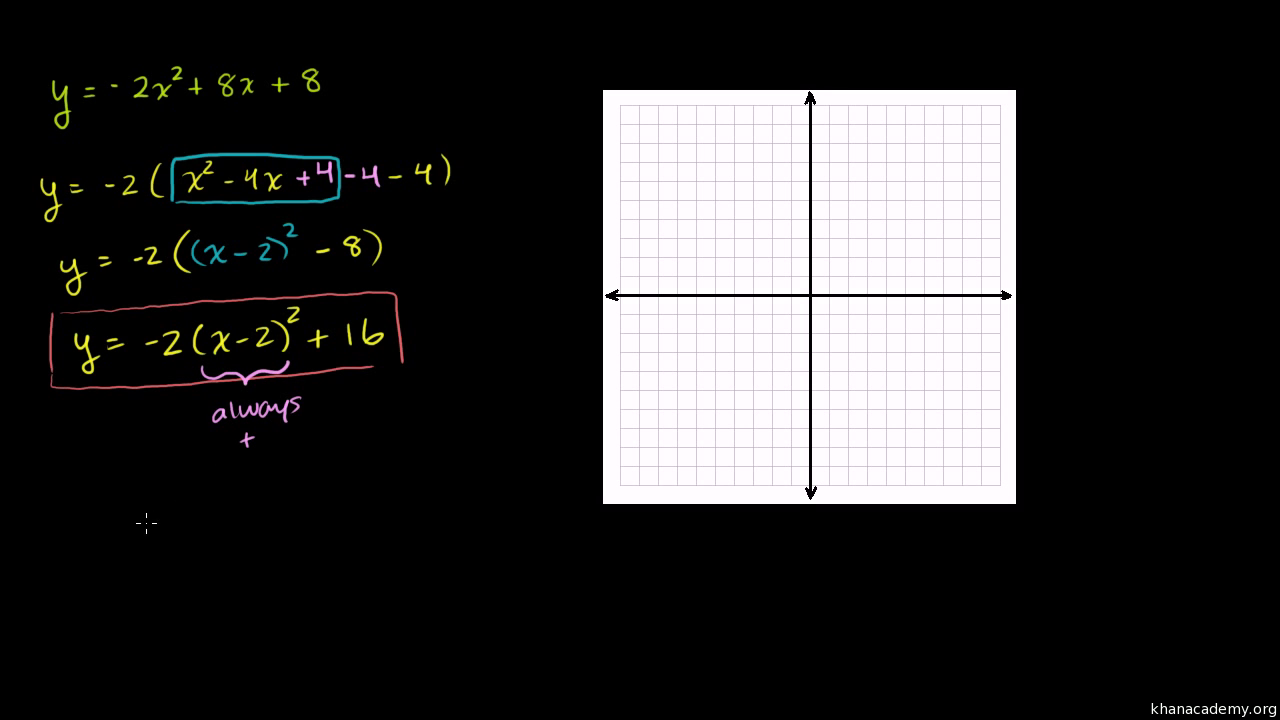
The vertex form of a parabola's equation is generally expressed as y = a(xh) 2 k (h,k) is the vertex as you can see in the picture below If a is positive then the parabola opens upwards like aThen the equation of the shifted directrix is y1 = 2 or y=1 The picture illustrates the shift of the parabola from standard position to the new position Similarly, if we are given an equation of the form y 2 A y B x C=0, we complete the square on the y terms and rewrite in the form ( yWhen graphing parabolas, find the vertex and yinterceptIf the xintercepts exist, find those as wellAlso, be sure to find ordered pair solutions on either side of the line of symmetry, x = − b 2 a Use the leading coefficient, a, to determine if a
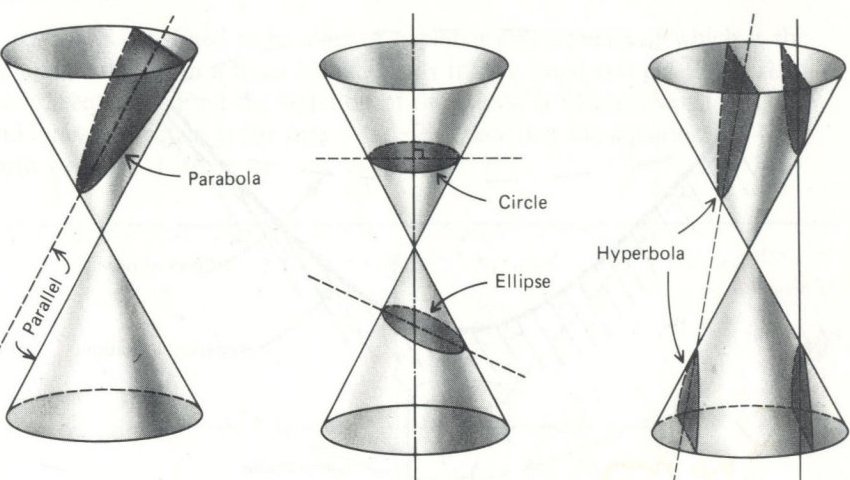
Son (x 1, 0) y (x 2, 0) El punto de corte con el eje de ordenadas viene por el punto (0, c) f(x) =x2 3x −4 g(x) =−x2 −x 6 y =−2x 5 Ejercicio 1 Representa gráficamente la función f(x) =−2x 4 Para dibujar una recta nf(x)=mx es necesario estudiar la pendiente m que nos dira si es creciente o decreciente la función Determinar el punto de corte con el eje de ordenadas que esConsider the parabola y = x 2 Since all parabolas are similar, this simple case represents all others Construction and definitions The point E is an arbitrary point on the parabola The focus is F, the vertex is A (the origin), and the line FA is the axis of symmetry The line EC is parallel to the axis of symmetry and intersects the x axis Solo llevas a la ecuación a la forma genérica de la ecuación de una parábola y= 2x^2x2y= 2(x^2x/21) , saco factor común 2y= 2(x^2x/21 1/16 1/16) , Hola0002 Hola0002 Matemáticas Bachillerato contestada El vertice de la parábola que corresponde a la función y=2x^2x2 es A (1/4, 19/8) B (1/4, 19/8) C (1/4, 15/8)
Parabola y=x^2 1 y=19-(x)^2のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 1 |  1 |  1 |
 1 |  1 |  1 |
 1 | 1 |  1 |
 1 |  1 | 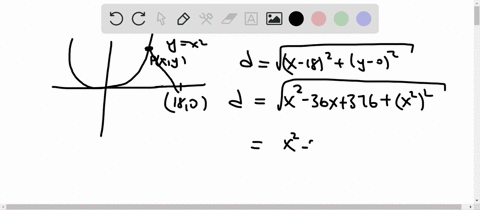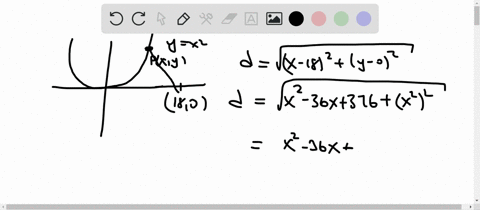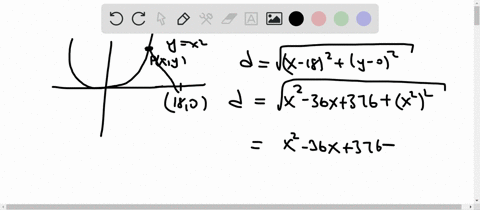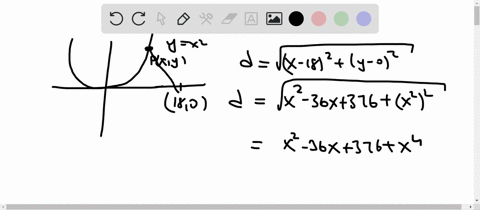 1 |
 1 | 1 | 1 |
 1 |  1 |  1 |
1 | 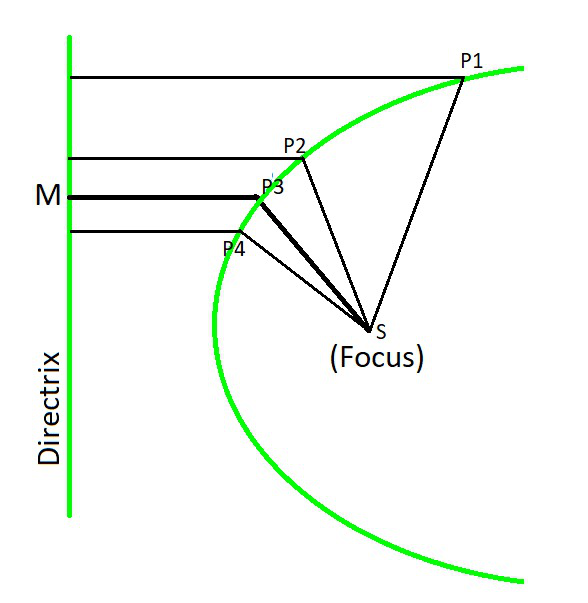 1 |  1 |
 1 | 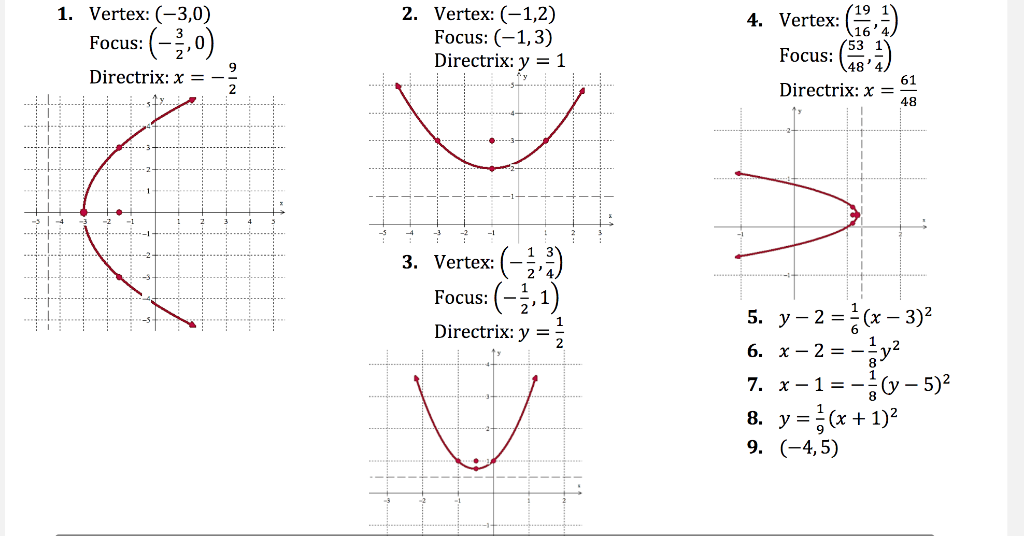1 |  1 |
 1 | 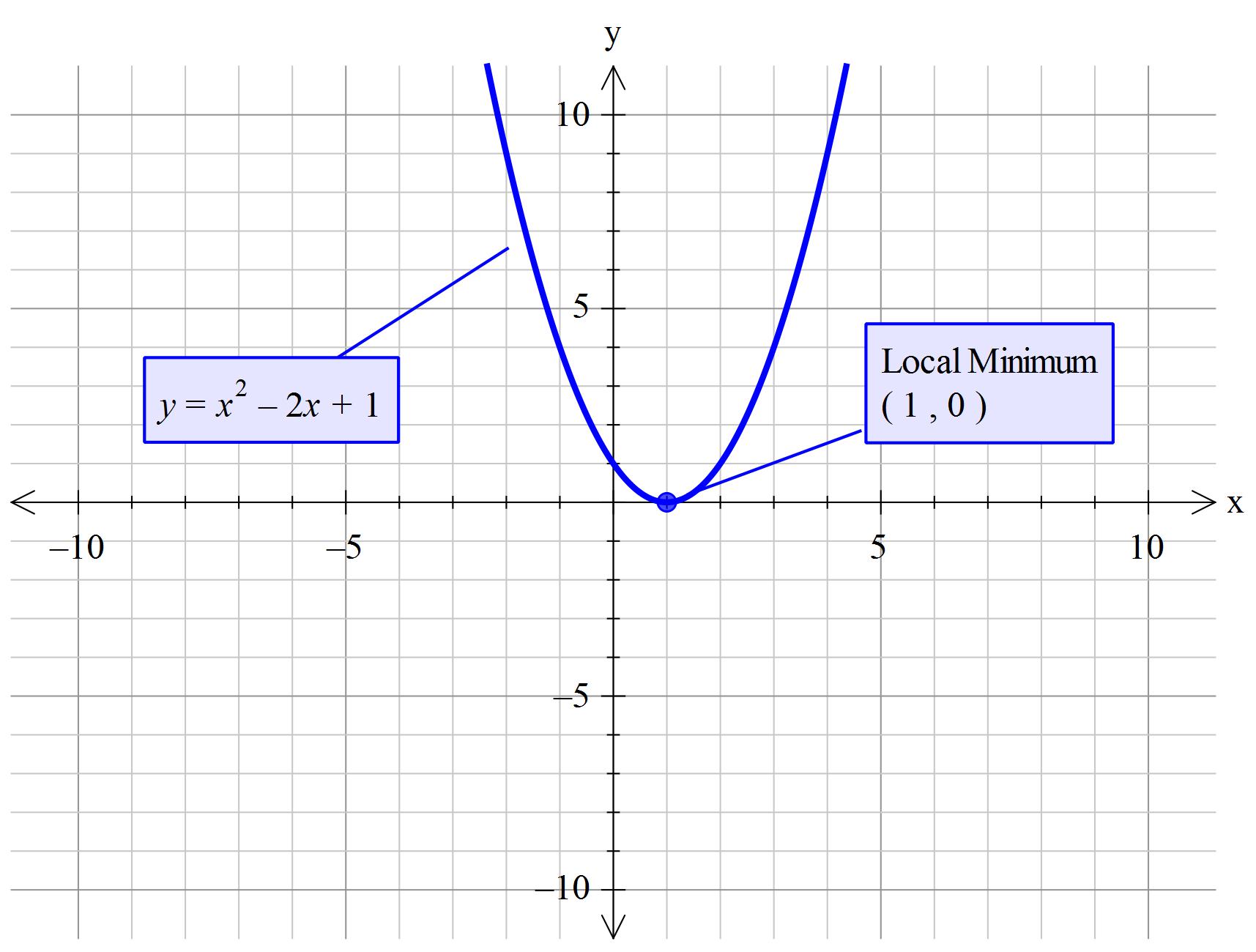 1 |  1 |
 1 |  1 |  1 |
1 |  1 |  1 |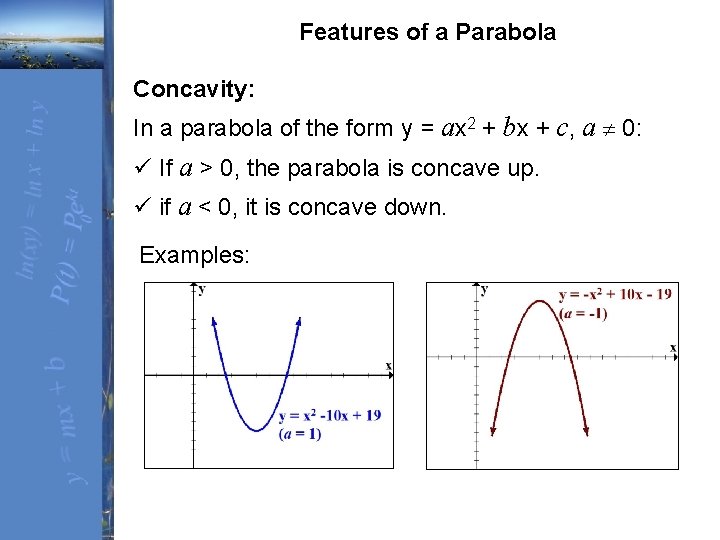
1 |  1 |  1 |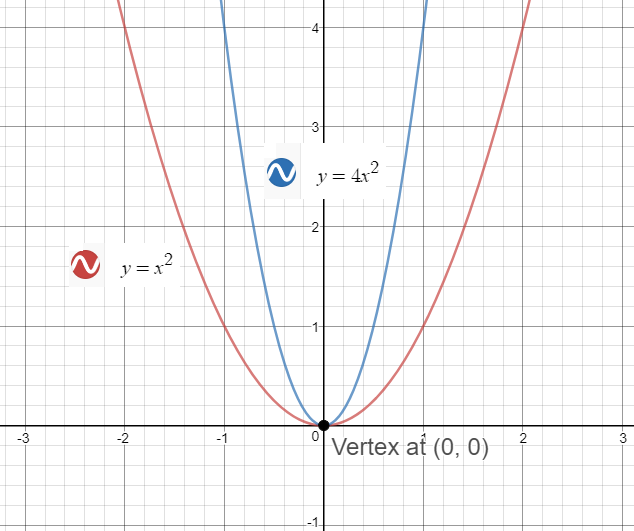
 1 |  1 | 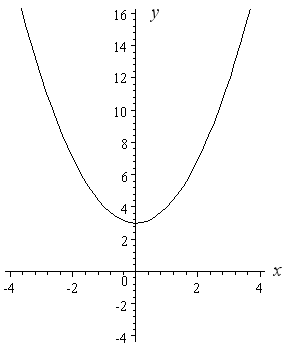 1 |
 1 |  1 | 1 |
1 | 1 | 1 |
 1 |  1 |  1 |
 1 |  1 |  1 |
1 | 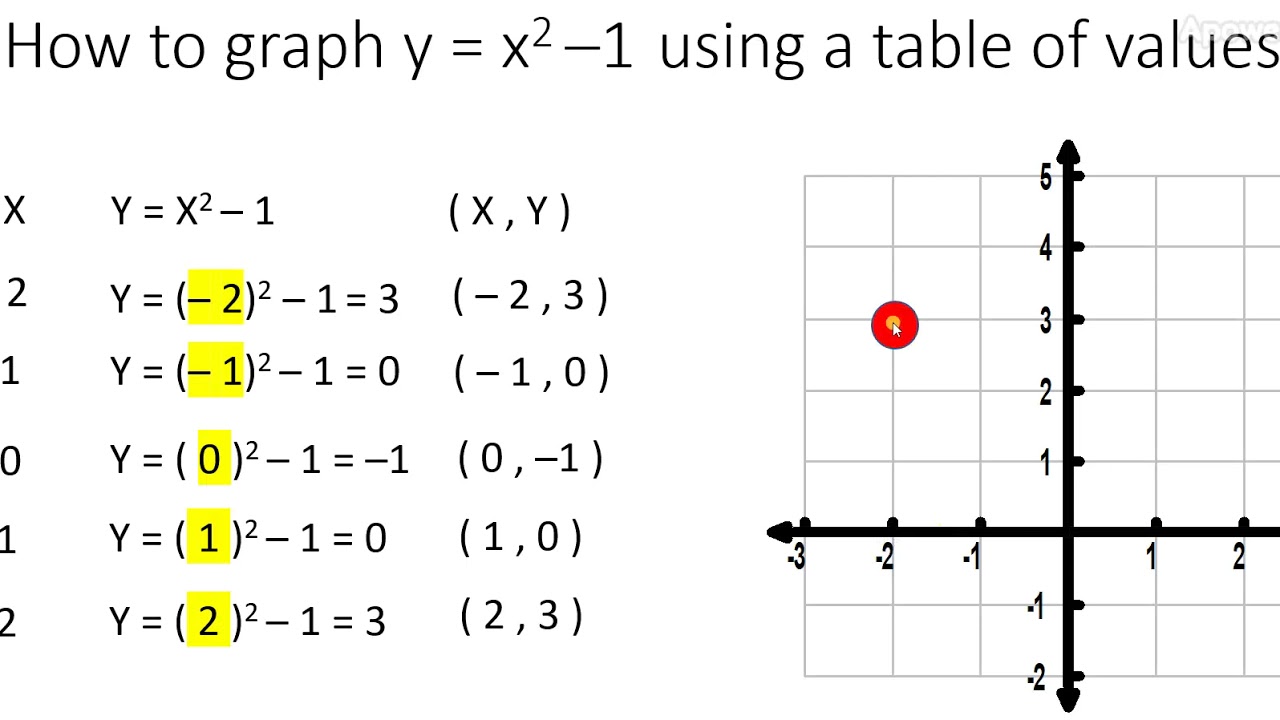 1 |  1 |
 1 |  1 |  1 |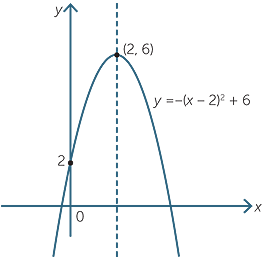
 1 |  1 |  1 |
 1 | 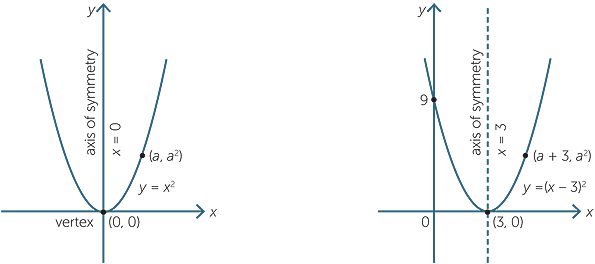 1 | 1 |
 1 | 1 | 1 |
 1 | 1 | 1 |
 1 |  1 |  1 |
 1 |  1 | 1 |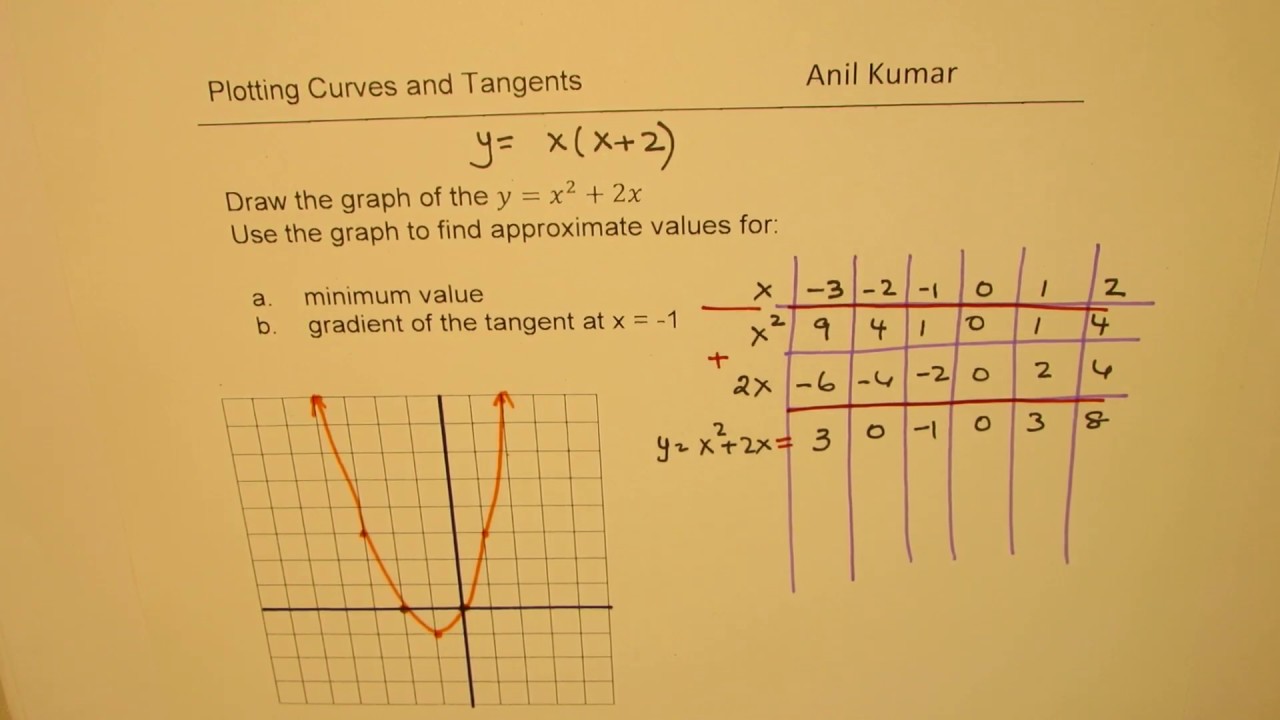
1 |  1 |  1 |
 1 |  1 |  1 |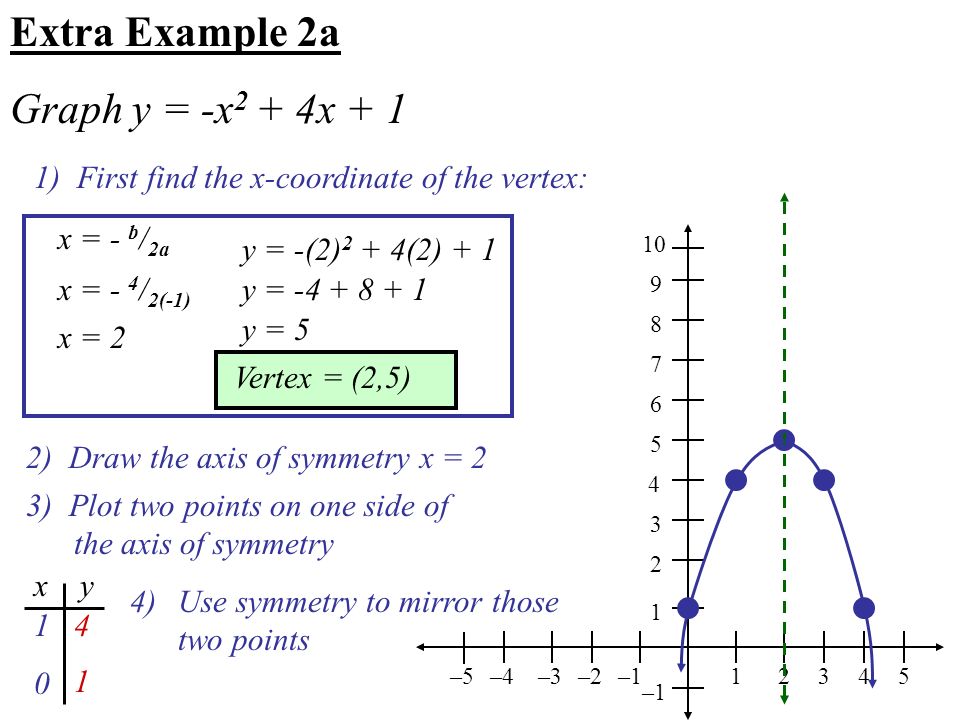
 1 |  1 |  1 |
 1 |  1 | 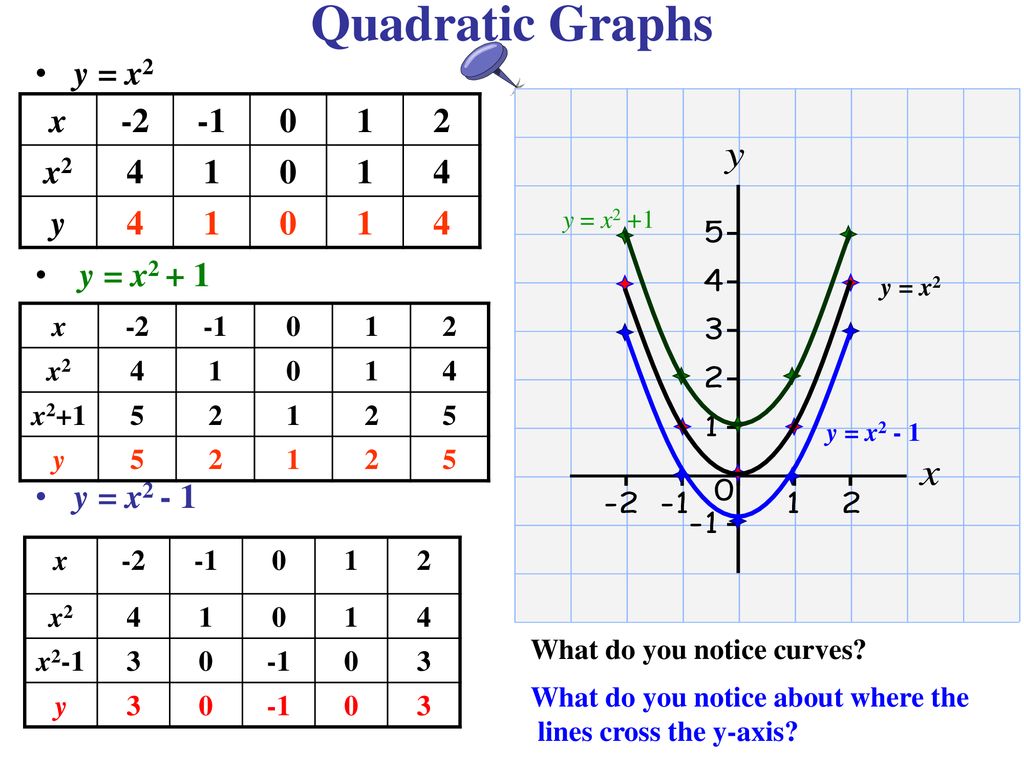 1 |
1 |  1 |  1 |
1 | 1 | 1 |
 1 | 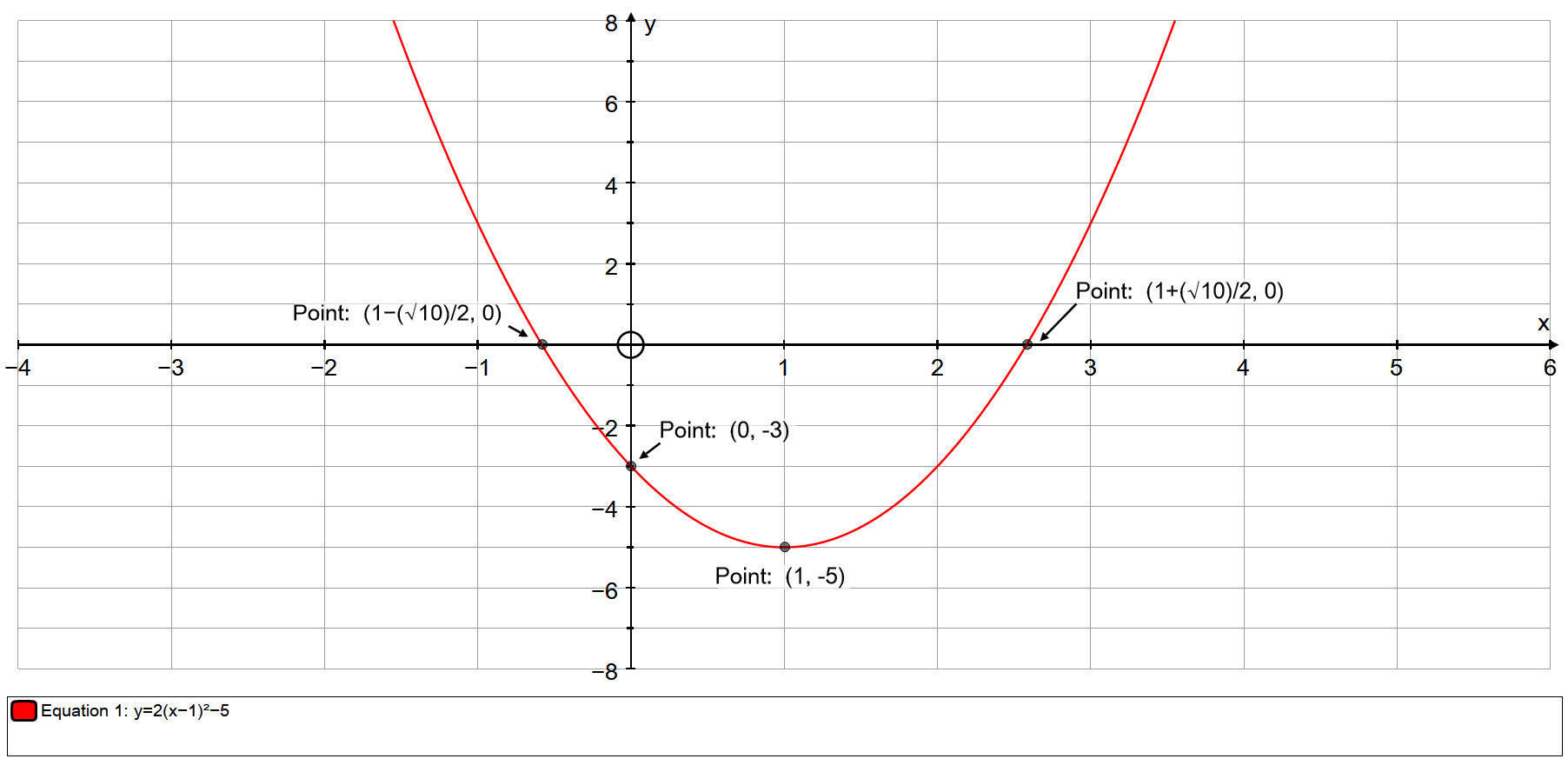 1 |  1 |
1 | 1 | 1 |
 1 |  1 | 1 |
 1 |  1 |
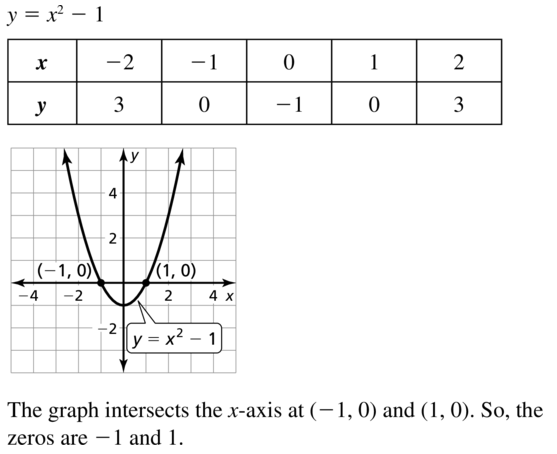
Step 1 Create a data table as shown below Notice that the column E contains values for x2 y = x2 is the Parent Function for a quadratic equation The graph of y = x2 is useful in understanding the behavior of the function given y = 4x2 Since, the sign of the x2 term is positive, the parabola opens up and we have a Minimum point at the Vertex You can find the coordinates of your vertex either using a mnemonic or the derivative 1) Mnemonic the coordinates of the vertex of a parabola in the form y = ax2 bx c are xv = − b 2a yv = − Δ 4a where Δ = b2 − 4ac in your case xv = 2 yv = −1
0 件のコメント:
コメントを投稿